Analytic Inverse Kinematics v1.1
Analytic Inverse Kinematics
Inverse kinematics described in this technical paper uses an analytic method and is calculated based on standard DH parameters.
Standard D-H Parameter
- A rotation 𝜃𝑖 about 𝑧𝑖−1 axis
- A translation 𝑑𝑖 along the 𝑧𝑖−1 axis
- A translation 𝑎𝑖 along the 𝑥𝑖−1 axis
- A rotation 𝛼𝑖 about 𝑥𝑖−1 axis
| d1 | d2 | d3 | d4 | d5 | d6 | a1 | a2 | |
|---|---|---|---|---|---|---|---|---|
| RB5-850 | 169.2 | 148.4 | 148.4 | 110.7 | 110.7 | 96.7 | 425.0 | 392.0 |
| RB3-1200 | 169.2 | 148.4 | 148.4 | 110.7 | 110.7 | 96.7 | 566.9 | 522.4 |
| RB10-1300 | 197.0 | 187.5 | 148.4 | 117.15 | 117.15 | 115.3 | 612.7 | 570.15 |
| Standard(Spong) | ||||
|---|---|---|---|---|
| link i | θi | di | ai | αi |
| L1 | θ1 | d1 | 0 | -90 |
| L2 | θ2 - 90 | -d2 | 0 | 0 |
| L3 | 0 | 0 | a1 | 0 |
| L4 | θ3 | d3 | 0 | 0 |
| L5 | 0 | 0 | a2 | 0 |
| L6 | θ4 + 90 | -d4 | 0 | 0 |
| L7 | 0 | 0 | 0 | 90 |
| L8 | θ5 | d5 | 0 | -90 |
| L9 | θ6 | -d6 | 0 | 90 |

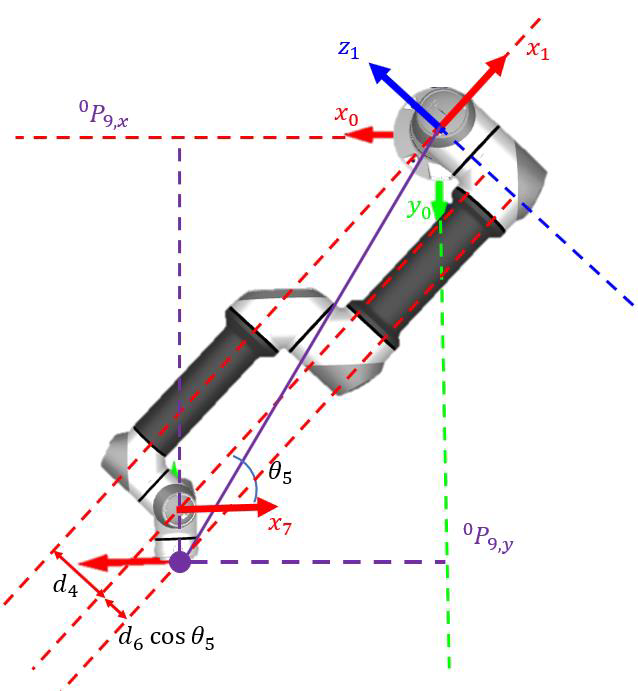
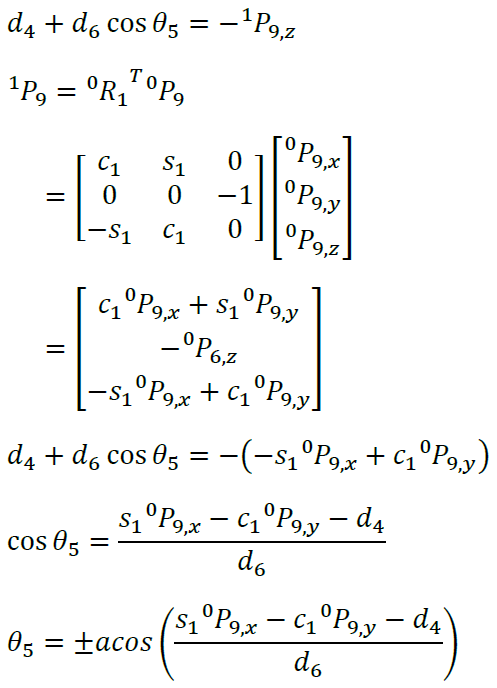
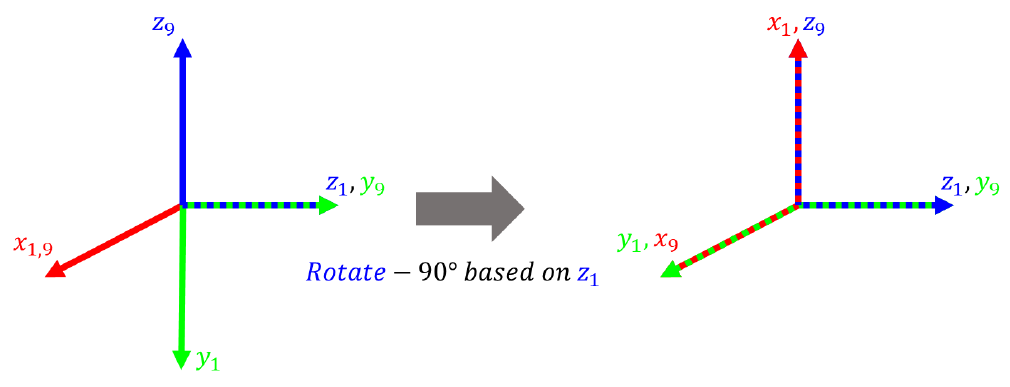
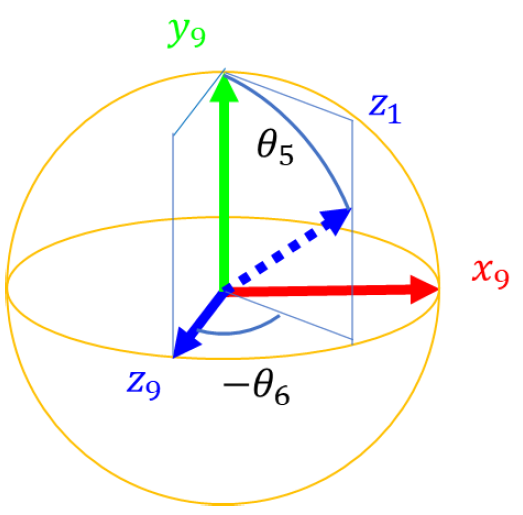
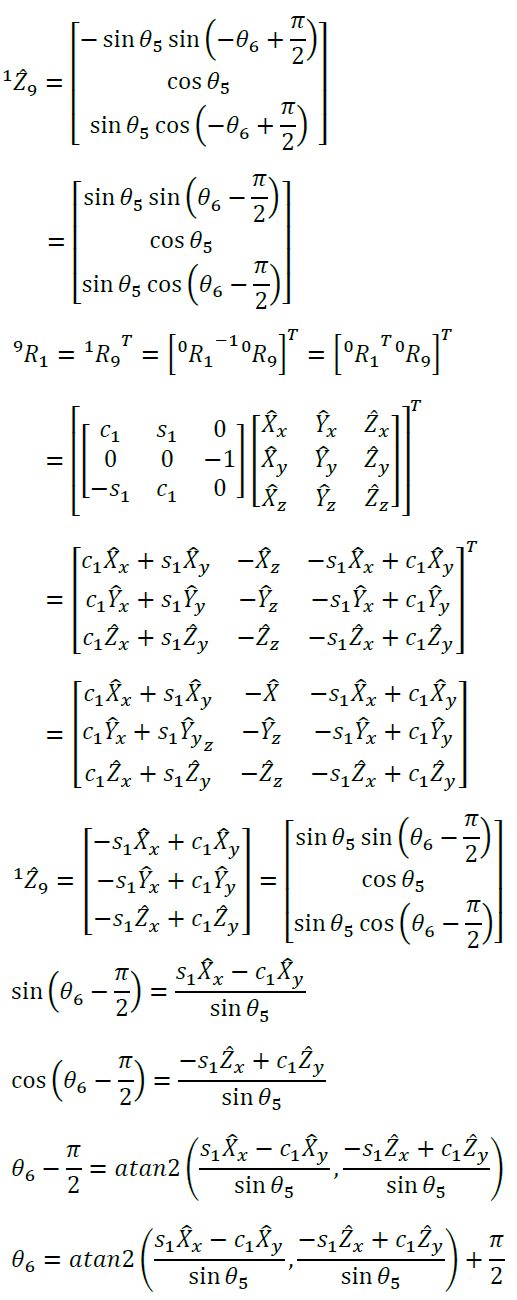
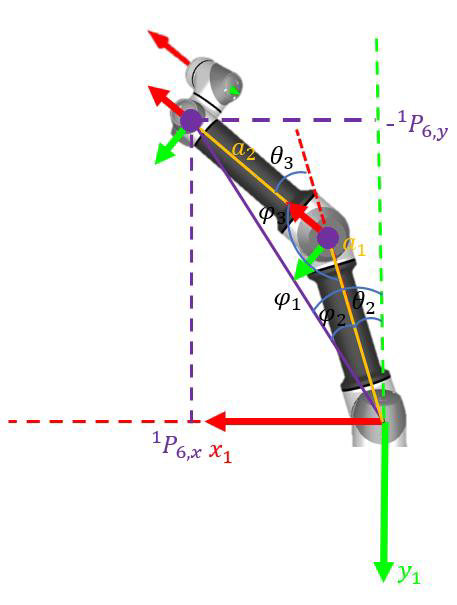
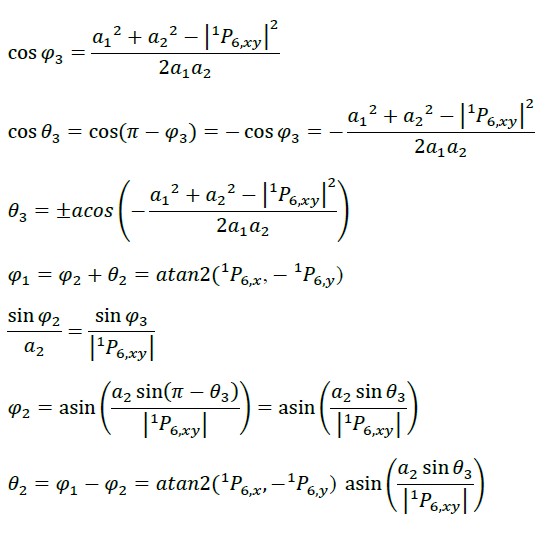
Because coordinate system 5 and coordinate system 6 differ by 90 degrees,
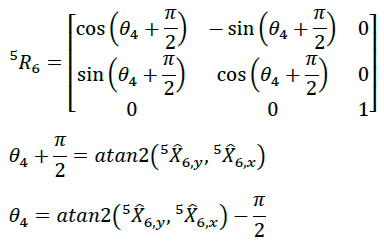
MATLAB
% -------------------------------------------------
% Rainbow Robotics
% Analytic Inverse Kinematics Example Code (based on Octave)
% All Right Reserved.
% -------------------------------------------------
clc; clear all; close all;
% -------------------------------------------------
D2R = pi/180.;
R2D = 180./pi;
% -------------------------------------------------
disp('---------------------------------');
disp('Input Cartesian Value (mm & deg)');
disp('---------------------------------');
% Rainbow Robotics use ZYX euler notation
% Z -> Y' -> X''
input_x = -156.76
input_y = -155.15
input_z = 814.96
input_rx = -43.47
input_ry = 80.56
input_rz = -60.88
% -------------------------------------------------
x = input_x;
y = input_y;
z = input_z;
rx = input_rx*D2R;
ry = input_ry*D2R;
rz = input_rz*D2R;
% -------------------------------------------------
% Link Length parameter (RB5-850)
d1 = 169.2;
d2 = 148.4;
d3 = 148.4;
d4 = 110.7;
d5 = 110.7;
d6 = 96.7;
a1 = 425.0;
a2 = 392.0;
% -------------------------------------------------
Rz = [cos(rz) -sin(rz) 0;
sin(rz) cos(rz) 0;
0 0 1;];
Ry = [cos(ry) 0 sin(ry);
0 1 0;
-sin(ry) 0 cos(ry);];
Rx = [1 0 0;
0 cos(rx) -sin(rx);
0 sin(rx) cos(rx);];
R = Rz * Ry * Rx;
% -------------------------------------------------
Y06 = R(:, 2);
P06 = [x;y;z];
P05 = P06 + d6*Y06;
th1 = atan2(P05(2), P05(1)) - acos(d4/sqrt(P05(2)^2 + P05(1)^2))+0.5*pi;
th5 = +acos((sin(th1)*P06(1)-cos(th1)*P06(2)-d4)/d6);
th6 = atan2(-(-sin(th1)*R(1,1)+cos(th1)*R(2,1))/sin(th5), (-sin(th1)*R(1,3)+cos(th1)*R(2,3))/sin(th5))+0.5*pi;
A01 = [cos(th1) -cos(-pi*0.5)*sin(th1) sin(-pi*0.5)*sin(th1) 0;
sin(th1) cos(-pi*0.5)*cos(th1) -sin(-pi*0.5)*cos(th1) 0;
0 sin(-pi*0.5) cos(-pi*0.5) d1;
0 0 0 1];
A67 = [cos(0) -cos(pi*0.5)*sin(0) sin(pi*0.5)*sin(0) 0;
sin(0) cos(pi*0.5)*cos(0) -sin(pi*0.5)*cos(0) 0;
0 sin(pi*0.5) cos(pi*0.5) 0;
0 0 0 1];
A78 = [cos(th5) -cos(-pi*0.5)*sin(th5) sin(-pi*0.5)*sin(th5) 0;
sin(th5) cos(-pi*0.5)*cos(th5) -sin(-pi*0.5)*cos(th5) 0;
0 sin(-pi*0.5) cos(-pi*0.5) d5;
0 0 0 1];
A89 = [cos(th6) -cos(pi*0.5)*sin(th6) sin(pi*0.5)*sin(th6) 0;
sin(th6) cos(pi*0.5)*cos(th6) -sin(pi*0.5)*cos(th6) 0;
0 sin(pi*0.5) cos(pi*0.5) -d6;
0 0 0 1];
A17 = inv(A01)*[R P06;0 0 0 1]*inv(A89)*inv(A78)*inv(A67);
P14 = [A17(1,4);
A17(2,4);
A17(3,4)];
th3 = +acos((P14(1)^2+P14(2)^2-a1^2-a2^2)/(2*a1*a2));
th2 = atan2(P14(1), -P14(2))-asin(a2*sin(th3)/sqrt(P14(1)^2+P14(2)^2));
A12 = [cos(th2-pi*0.5) -cos(0)*sin(th2-pi*0.5) sin(0)*sin(th2-pi*0.5) 0;
sin(th2-pi*0.5) cos(0)*cos(th2-pi*0.5) -sin(0)*cos(th2-pi*0.5) 0;
0 sin(0) cos(0) -d2;
0 0 0 1];
A23 = [cos(0) -cos(0)*sin(0) sin(0)*sin(0) a1*cos(0);
sin(0) cos(0)*cos(0) -sin(0)*cos(0) a1*sin(0);
0 sin(0) cos(0) 0;
0 0 0 1];
A34 = [cos(th3) -cos(0)*sin(th3) sin(0)*sin(th3) 0;
sin(th3) cos(0)*cos(th3) -sin(0)*cos(th3) 0;
0 sin(0) cos(0) d3;
0 0 0 1];
A45 = [cos(0) -cos(0)*sin(0) sin(0)*sin(0) a2*cos(0);
sin(0) cos(0)*cos(0) -sin(0)*cos(0) a2*sin(0);
0 sin(0) cos(0) 0;
0 0 0 1];
A56_cal = inv(A45)*inv(A34)*inv(A23)*inv(A12)*inv(A01)*[R P06;0 0 0 1]*inv(A89)*inv(A78)*inv(A67);
th4 = atan2(A56_cal(2,1), A56_cal(1,1))-0.5*pi;
% -------------------------------------------------
disp('---------------------------------');
disp('Inverse Kinematics Result (deg)');
disp('---------------------------------');
th1 = th1 * R2D
th2 = th2 * R2D
th3 = th3 * R2D
th4 = th4 * R2D
th5 = th5 * R2D
th6 = th6 * R2D Rainbow Robotics
Rainbow Robotics